이산수학의 함수 챕터를 공부하다가 팩토리얼의 '재귀적 정의'를 보고 왜 굳이 이렇게 정의를 해야 하는지 의문이 생겼다.
팩토리얼은 지난 글에서도 한 번 다뤘지만 이번엔 좀 다른 관점에서 바라보려고 한다.
팩토리얼이란?
팩토리얼은 양의 정수 에 대해 라고 쓰고, 1부터 n까지의 모든 정수를 곱한 값이다. 수식으로 보면 다음과 같다.
n!=1×2×3×⋯×n
그리고 하나 기억할 것은, 수학에서는 0!=1 로 정의되어 있다는 것이다. 이게 앞으로 다룰 재귀적 정의에서 중요한 역할을 하게 된다.
재귀적 정의, 팩토리얼의 마법 공식
팩토리얼을 계산하는 방법은 여러 가지가 있지만, 오늘의 주인공은 재귀적 정의이다.
재귀(recursion)는 어떤 문제를 해결하기 위해 그 문제의 더 작은 버전을 반복적으로 해결하는 방식이다. 수학이나 코딩에서 재귀적이라고 할 때는, 어떤 함수나 정의가 자기 자신을 호출하거나 참조하면서 문제를 해결하는 구조를 말한다.
팩토리얼의 재귀적 정의는 이렇게 표현된다.
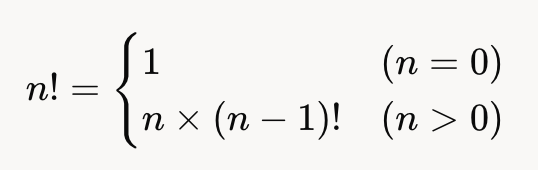
팩토리얼의 경우, n!을 계산하기 위해 (n-1)!을 계산하고, 다시 (n-1)!을 계산하기 위해 (n-2)!을 계산하는 식으로 진행된다. 이것이 바로 재귀적인 접근이다.
-
기저 조건(Base Case): n=0 일 때 0!=1로 재귀가 멈추는 조건.
-
재귀 단계(Recursive Case): n>0 일 때 n!=n×(n−1)! 즉 하위 문제인 (n−1)! 을 풀어서 답을 구함.
- 자기 참조(Self-Reference): n!을 계산하기 위해 (n-1)!을 호출함. 즉, 팩토리얼 정의가 자기 자신을 참조하는 구조.
예를 들어 3! 을 계산해보자.
3!=3×2!
2!=2×1!
1!=1×0!
0!=1 (기저 조건)
이걸 거꾸로 올라가면서 계산해보면 다음과 같이 답이 구해진다.
1!=1×1=1
2!=2×1=2
3!=3×2=6
이처럼 문제를 하위 문제로 나누고, 그 하위 문제를 더 작은 하위 문제로 나누는 과정이 반복되다가 기저 조건에서 멈추는 구조 때문에 재귀적이라고 한다.
팩토리얼을 파이썬으로 구현하기
파이썬은 직관적으로 재귀를 구현하기 좋은 언어다.
팩토리얼을 재귀적으로 구현한 파이썬 코드는 다음과 같다.
def factorial(n):
if n == 0: # 기저 조건
return 1
else: # 재귀 단계
return n * factorial(n-1)
이 코드를 실행해보면 결과는 다음과 같다.
print(factorial(3)) # 출력: 6
print(factorial(5)) # 출력: 120
print(factorial(0)) # 출력: 1
동작 과정 :
예시로 factorial(3)을 호출하면 어떻게 작동하는 지 단계별로 살펴보자.
- 첫 번째 호출: factorial(3)
- n = 3, 기저 조건(n == 0)에 해당하지 않으므로 else로 이동.
- return 3 * factorial(2)를 계산해야 함.
- 아직 factorial(2)의 값을 모르므로 factorial(2)를 호출.
- 두 번째 호출: factorial(2)
- n = 2, 기저 조건에 해당하지 않음.
- return 2 * factorial(1)을 계산.
- factorial(1)을 호출.
- 세 번째 호출: factorial(1)
- n = 1, 기저 조건에 해당하지 않음.
- return 1 * factorial(0)을 계산.
- factorial(0)을 호출.
- 네 번째 호출: factorial(0)
- n = 0, 기저 조건(n == 0)에 해당.
- return 1을 반환.
- 재귀가 여기서 멈춤.
- 역순으로 계산 시작 (재귀 풀기):
- factorial(0)이 1을 반환했으므로, factorial(1)은 1 * 1 = 1.
- factorial(1)이 1을 반환했으므로, factorial(2)는 2 * 1 = 2.
- factorial(2)가 2를 반환했으므로, factorial(3)은 3 * 2 = 6.
- 최종 결과:
- factorial(3)은 6을 반환.
- 즉, 3! = 3 × 2 × 1 = 6.
동작 요약
- 함수는 n이 0이 될 때까지 자신을 재귀적으로 호출하며, 호출 스택에 factorial(n-1)을 쌓는다.
- 기저 조건에 도달하면 스택을 풀면서 각 단계의 값을 곱해 최종 결과를 계산한다.
재귀 함수 사용 시 주의할 점
재귀를 사용하면 코드가 간결하고 이해가 쉽다. 하지만 다음과 같은 점을 조심해야 한다.
- 기저 조건이 반드시 필요하다. 기저 조건이 없으면 재귀가 무한 반복되면서 프로그램이 멈추지 않는다.
위 코드에서 if n==0 조건을 빼면 n이 계속 줄어들다가 음수가 되면서 스택 오버플로우(stack overlow) 오류가 발생한다. 재귀는 반드시 멈출 지점이 있어야 한다. - 성능 문제도 생각해야 한다. 재귀는 함수를 반복적으로 호출하기 때문에 메모리를 많이 사용할 수 있다. 예를 들어 n이 너무 크면(ex. 1000!) 함수 호출이 너무 깊어져서 성능이 떨어질 수 있다. 이런 경우에는 반복문을 사용하는 게 더 효율적일 수 있다.
재귀 대신 반복문으로 팩토리얼을 구현한 코드
def factorial_iterative(n):
result = 1
for i in range(1, n + 1):
result *= i
return result
이 코드는 재귀 함수 대신 단순히 1부터 까지 곱하는 방식으로 동작한다.
성능 면에서는 더 효율적이지만, 재귀만큼 수학적 정의와 직관적으로 연결되지는 않는다.
재귀함수와 파이썬
재귀는 팩토리얼 같은 단순한 문제뿐만 아니라 더 복잡한 문제에서도 유용하다. 예를 들어, 트리 구조를 탐색하거나 피보나치 수열을 계산할 때도 재귀가 자주 쓰인다. 파이썬은 재귀를 지원하는 언어로, 이런 재귀적 사고를 코드로 표현하기 좋다.
하지만 파이썬에서는 재귀의 깊이 제한(recursion depth limit)이 있어서 너무 깊은 재귀 호출은 피해야 한다. 기본적으로 파이썬은 재귀 호출을 약 1000번 정도로 제한하는데, 이 한계를 넘어서면 RecursionError가 발생한다. 필요하다면 sys.setrecursionlimit()으로 이 한계를 조정할 수 있지만, 가능하면 반복문으로 해결하는 것이 안전할 것이다.
'KNOU CS > 이산수학' 카테고리의 다른 글
| 다익스트라(Dijkstra) 알고리즘으로 최단 경로 문제 해결하기 (0) | 2025.04.06 |
|---|---|
| [이산수학] 행렬곱은 어떻게 구할까? (feat. 펭귄 90도 회전시키기) (0) | 2025.03.11 |
| [이산수학] 조합(Combination) - feat. 계승(factorial) (2) | 2025.03.05 |


